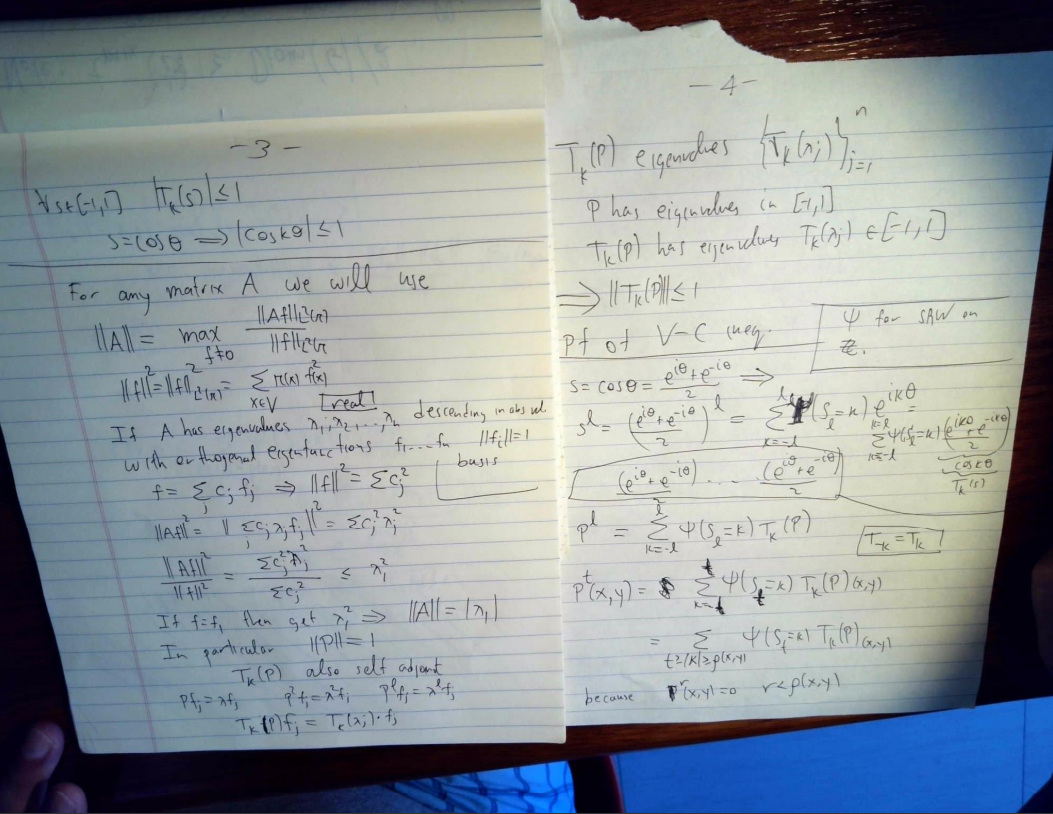1.* Let ![]() be the transition matrix corresponding to simple random walk on a finite connected graph
be the transition matrix corresponding to simple random walk on a finite connected graph ![]() . Show that for each
. Show that for each ![]() , we have
, we have ![]() . Moreover, if the graph is bipartite, then
. Moreover, if the graph is bipartite, then ![]() .
.
2.* Let ![]() . Consider a graph
. Consider a graph ![]() which consists of a complete graph on
which consists of a complete graph on ![]() nodes, and a path of length
nodes, and a path of length ![]() that emanates from one of them (call it
that emanates from one of them (call it ![]() ) and ends in a node
) and ends in a node ![]() . Give the best upper and lower bounds you can for
. Give the best upper and lower bounds you can for
(a) The maximal hitting time for SRW in ![]() .
.
(b) The maximal hitting time for SRW started from ![]() .
.
(c) The cover time for SRW in ![]() .
.
(d) The mixing time for SRW in ![]() .
.
You can safely ignore constant factors, but pay attention to the dependence on ![]() and
and ![]() .
.
3. Read and understand the computation of the eigenvalues and eigenvectors for simple random walk on the ![]() -cycle.
-cycle.