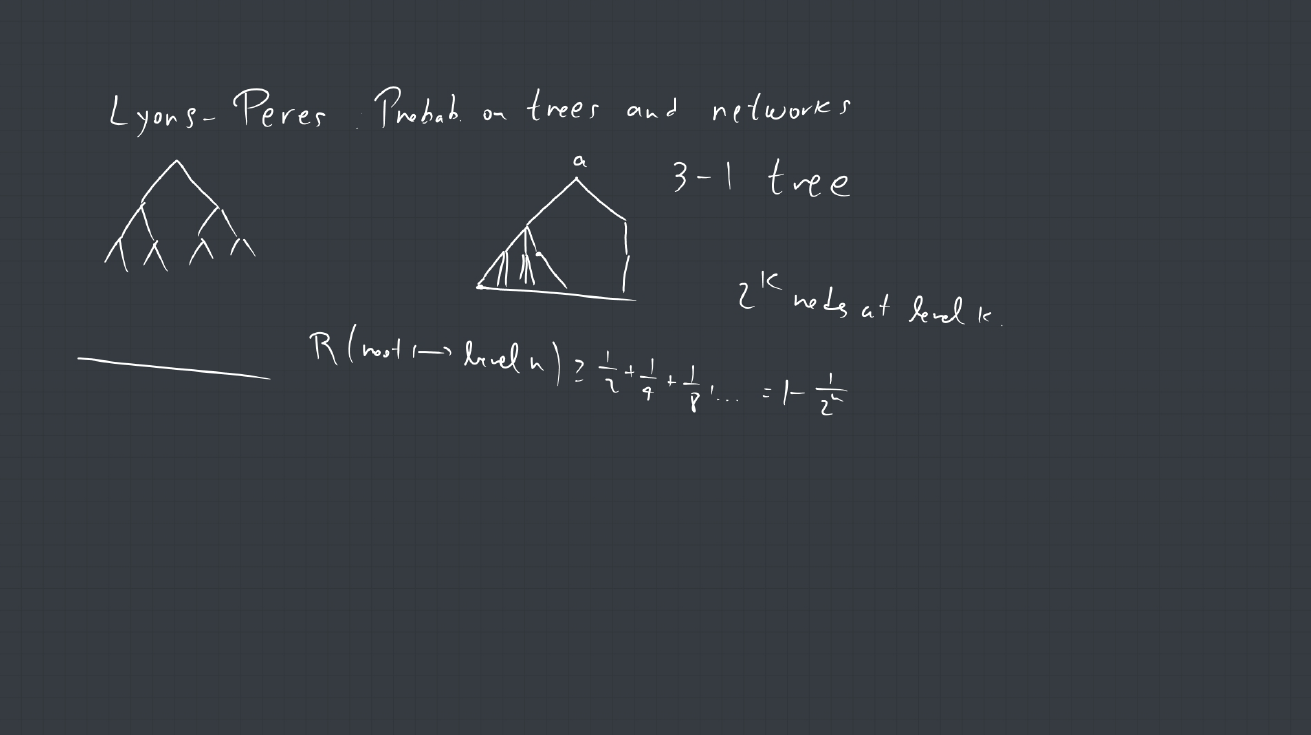1.* Let 
be the strong stationary time constructed in class for the reverse riffle shuffle, i.e., the first time that all cards have distinct label vectors. Is optimal? (i.e., does it have minimal expectation among all strong stationary times?)
If not, can you find another strong stationary time with a smaller expectation than ? If the answer is positive, can you find a halting state?
2*. Let 
and 
be opposite corners of an 
cube in the 3D lattice. Does the effective resistance between and tend to infinity as 
?
3*. In the 3-1 tree, the root has two children, and for each 
, half the vertices at level 
have three children and the other half have one child. Show that the effective resistance between the root and level 
of this tree tends to infinity as .
4. An Oregon professor has umbrellas, of which initially 
are at her office and 
are at her home. Every day, the professor walks to the office in the morning and returns home in the evening. In each trip, she takes an umbrella with her only if it is raining. Assume that in every trip between home and office or back, the chance of rain is 
, independently of other trips.
(a) Asymptotically, in what fraction of her trips does the professor get wet?
(b) Determine the expected number of trips until all umbrellas are at the same location.
(c) Determine the expected number of trips until the professor gets wet.