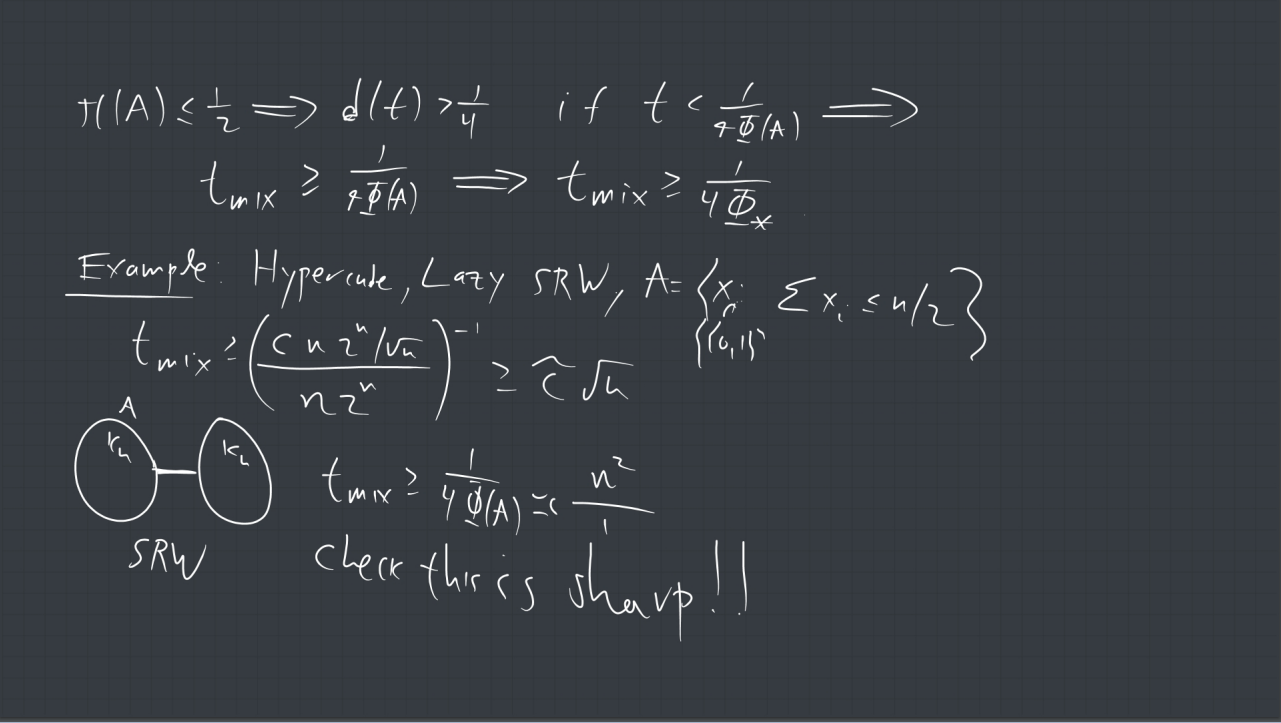1.* Let ![]() be simple random walk on the integers, with
be simple random walk on the integers, with ![]() . Show that
. Show that ![]() for all
for all ![]() . Hint: Prove the inequality
. Hint: Prove the inequality ![]() for all real
for all real ![]() , and use it to bound
, and use it to bound ![]() .
.
2.* Let ![]() be a b-ary tree of height
be a b-ary tree of height ![]() , that has
, that has ![]() vertices. What are the best upper and lower bounds you can prove for the mixing time of lazy SRW on
vertices. What are the best upper and lower bounds you can prove for the mixing time of lazy SRW on ![]() ?
?
3. Let ![]() be the set of invertible
be the set of invertible ![]() matrices mod 2. Find the cardinality of
matrices mod 2. Find the cardinality of ![]() . Hint: consider choosing the rows of the matrix one by one.
. Hint: consider choosing the rows of the matrix one by one.
4.* Let ![]() be a subset of the group of permutations
be a subset of the group of permutations ![]() . consider the Markov chain on
. consider the Markov chain on ![]() obtained by picking a permutation
obtained by picking a permutation ![]() in
in ![]() uniformly at random (independently of previous
uniformly at random (independently of previous ![]() ), and defining
), and defining ![]() .
.
(a) Write a lower bound for the mixing time of this chain in terms of ![]() and
and ![]() .
.
(b) Suppose that ![]() consists of transpositions. What is the smallest possible size of
consists of transpositions. What is the smallest possible size of ![]() for which this chain is irreducible?
for which this chain is irreducible?
(c) If ![]() consists of transpositions, can this chain be aperiodic?
consists of transpositions, can this chain be aperiodic?
(d) Suppose that ![]() consists of all transpositions, and we consider the lazy version of the chain above. Can you improve the lower bound from part (a) in this case?
consists of all transpositions, and we consider the lazy version of the chain above. Can you improve the lower bound from part (a) in this case?