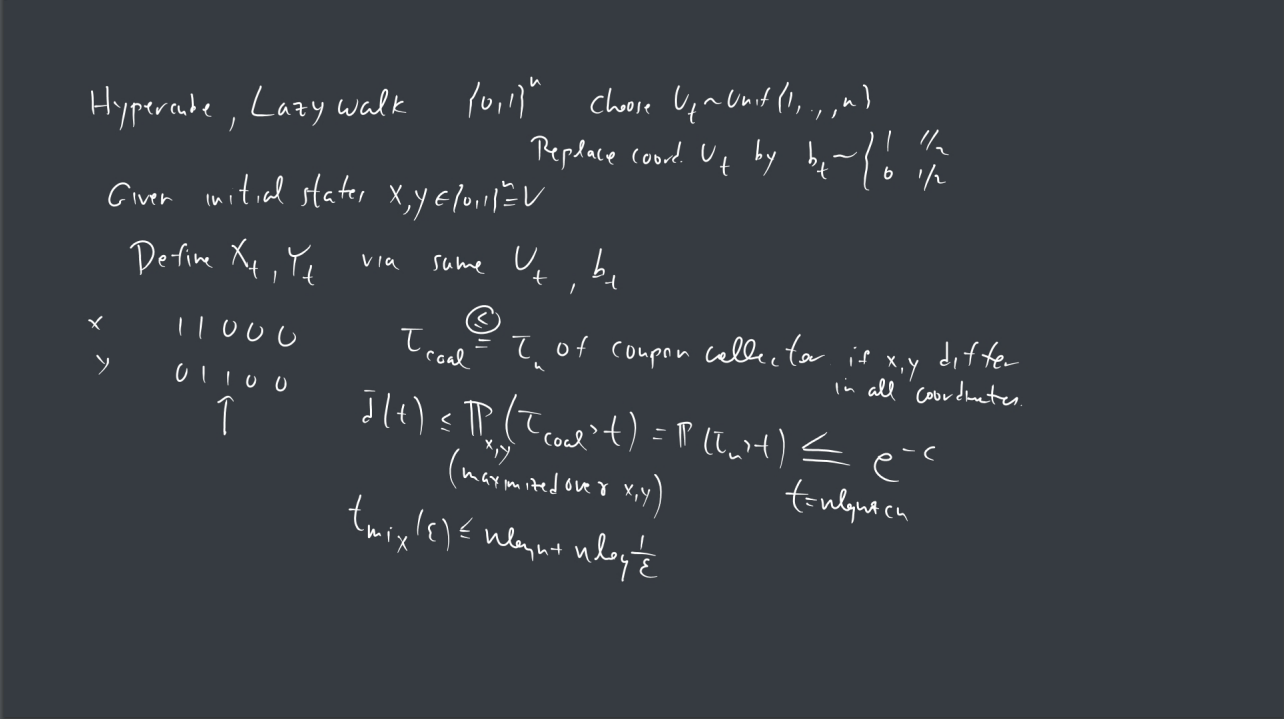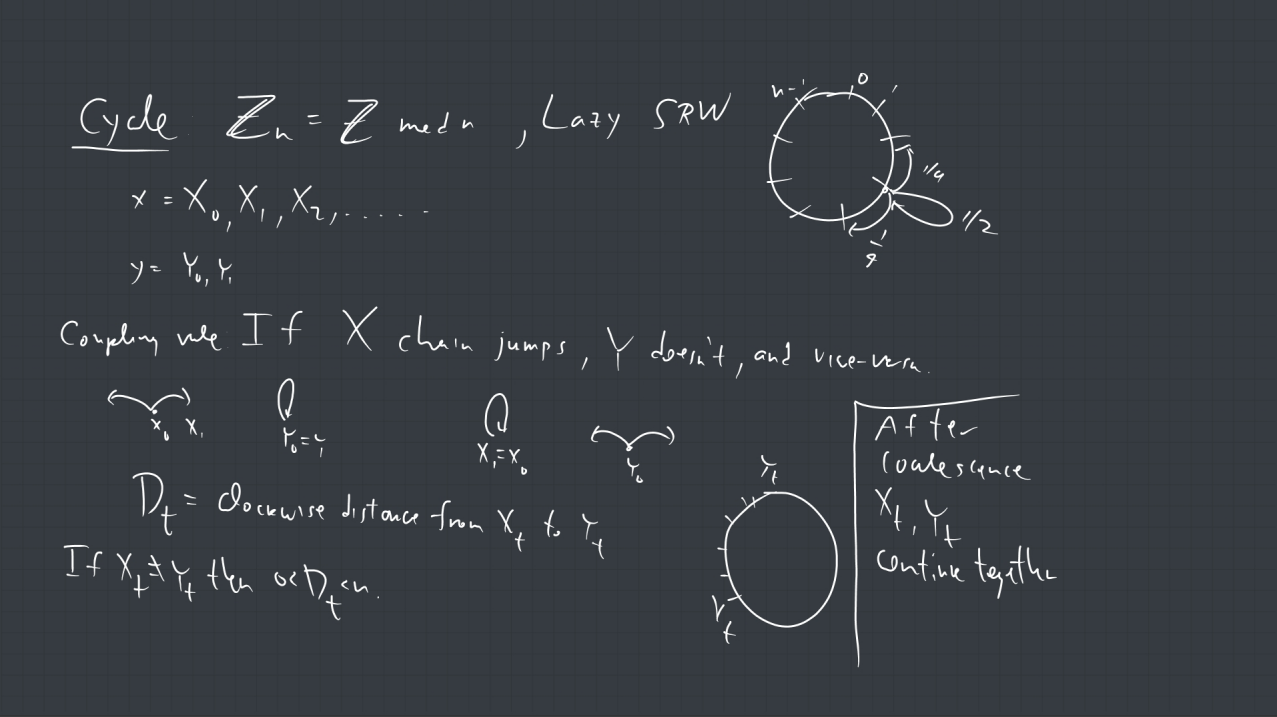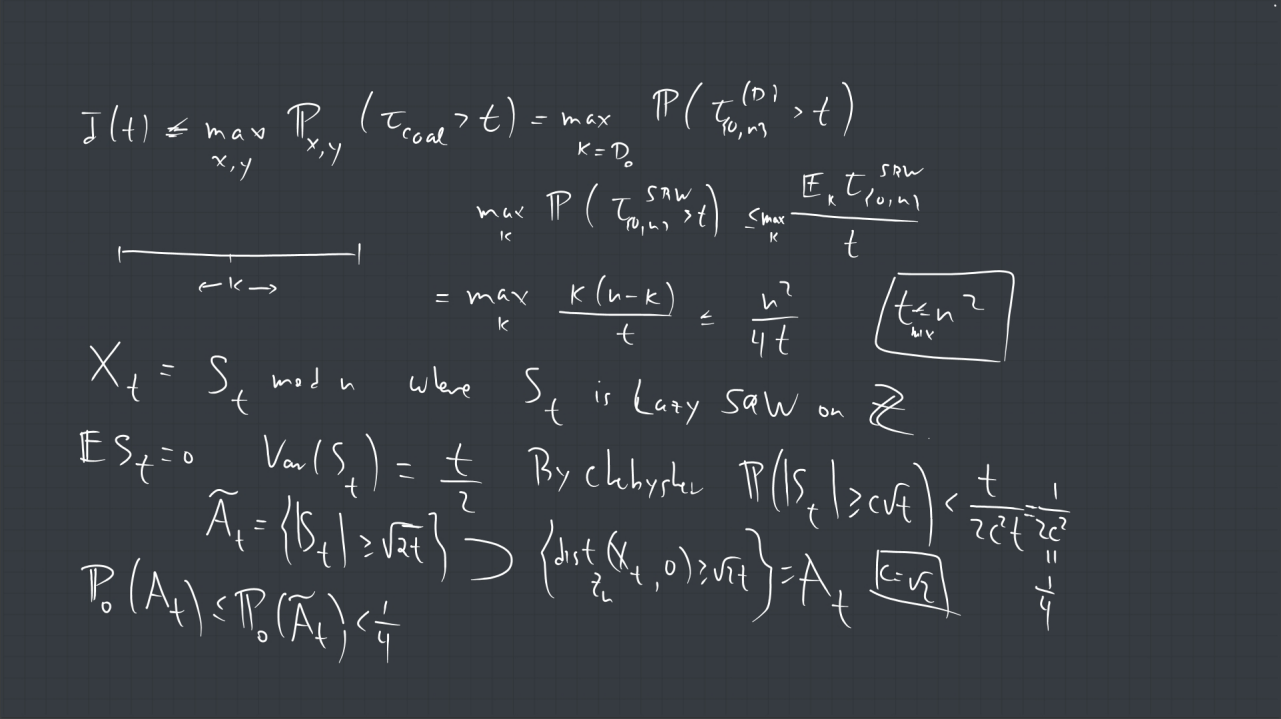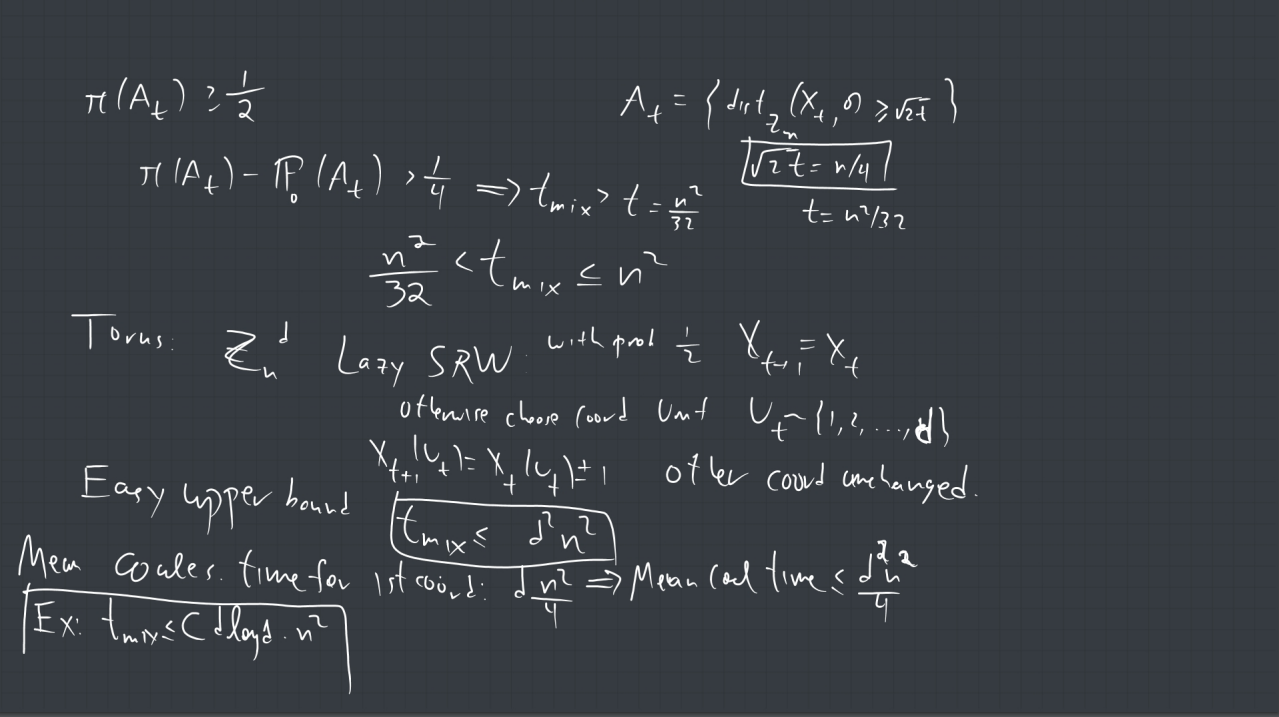1.* Let ![]() be simple random walk on the hypercube
be simple random walk on the hypercube ![]() , and let
, and let ![]() denote the Hamming weight (i.e., the number of ones) of
denote the Hamming weight (i.e., the number of ones) of ![]() . Then
. Then ![]() is also a Markov chain, with transition probabilities
is also a Markov chain, with transition probabilities ![]() and
and ![]() for
for ![]() . Read about projected (or lumped) chains on pages 23-25 of the textbook, and calculate
. Read about projected (or lumped) chains on pages 23-25 of the textbook, and calculate ![]() for
for ![]() . Hint: it suffices to calculate
. Hint: it suffices to calculate ![]() .
.
2. Show that the mixing time of lazy simple random walk on the discrete torus ![]() (see section 5.3.3 and Theorem 5.6 of the book) is
(see section 5.3.3 and Theorem 5.6 of the book) is ![]() .
.
3*. Consider the following Markov chain on the integers: Fix ![]() . Let
. Let ![]() for all integers
for all integers ![]() . Let
. Let ![]() . For which
. For which ![]() is the hitting time
is the hitting time ![]() finite almost surely, and what is its expectation
finite almost surely, and what is its expectation ![]() ?
?
A key issue is determining when the expectation is finite. It is OK to use the strong law of large numbers.
4. Given an irreducible aperiodic transition matrix ![]() , show that for any two states
, show that for any two states ![]() , there is a coupling of the chains
, there is a coupling of the chains ![]() started from
started from ![]() respectively, such that the expected coalescence time of these chains is at most
respectively, such that the expected coalescence time of these chains is at most ![]() .
.
5. Solve exercises 4.3 and 4.4 in the book, which can be found at https://www.yuval-peres-books.