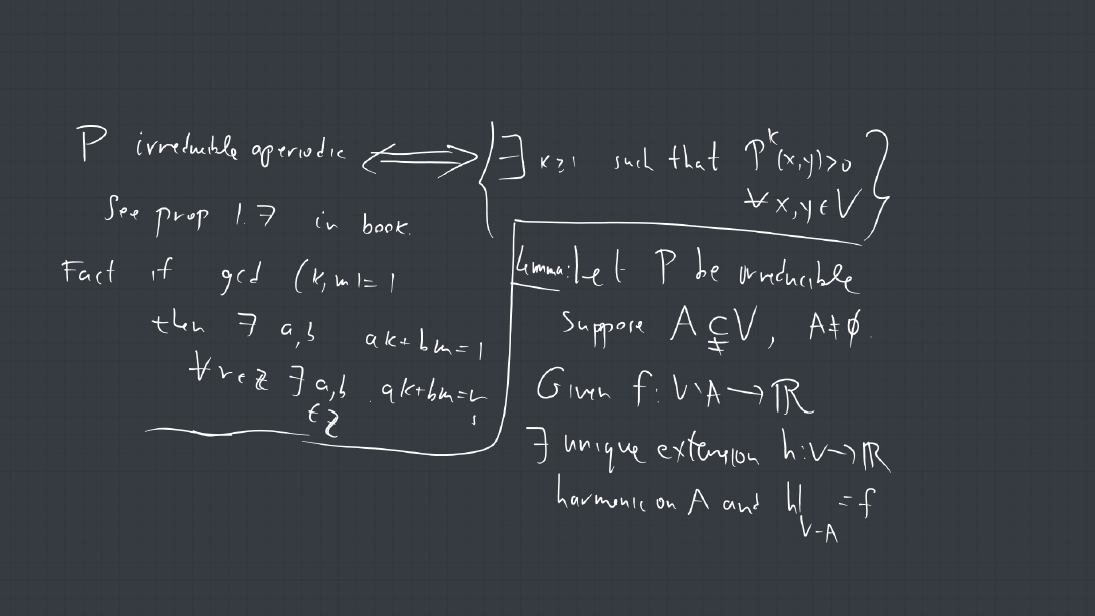
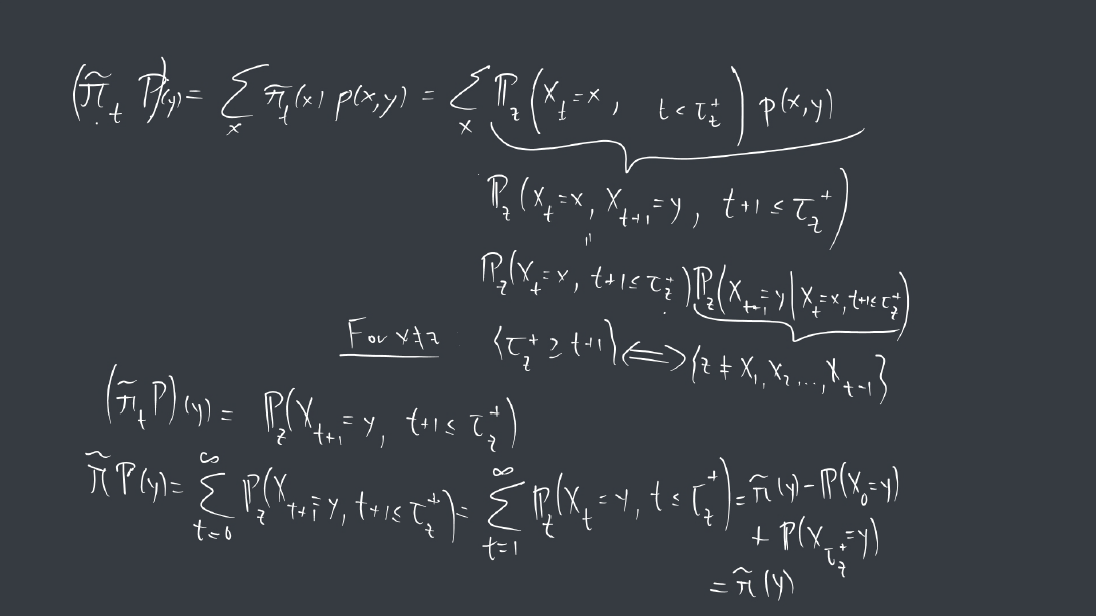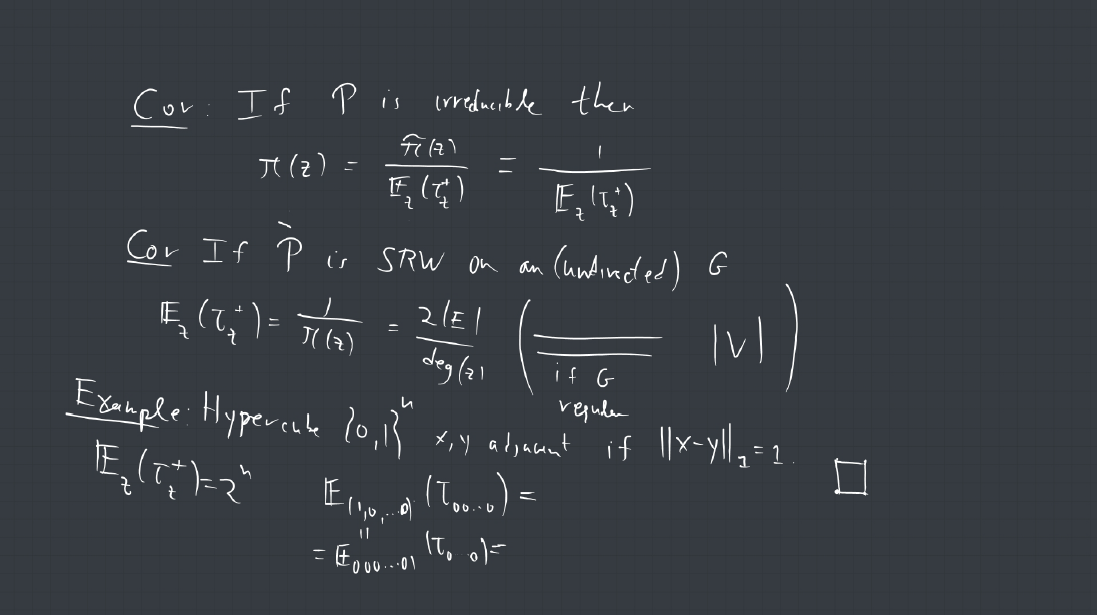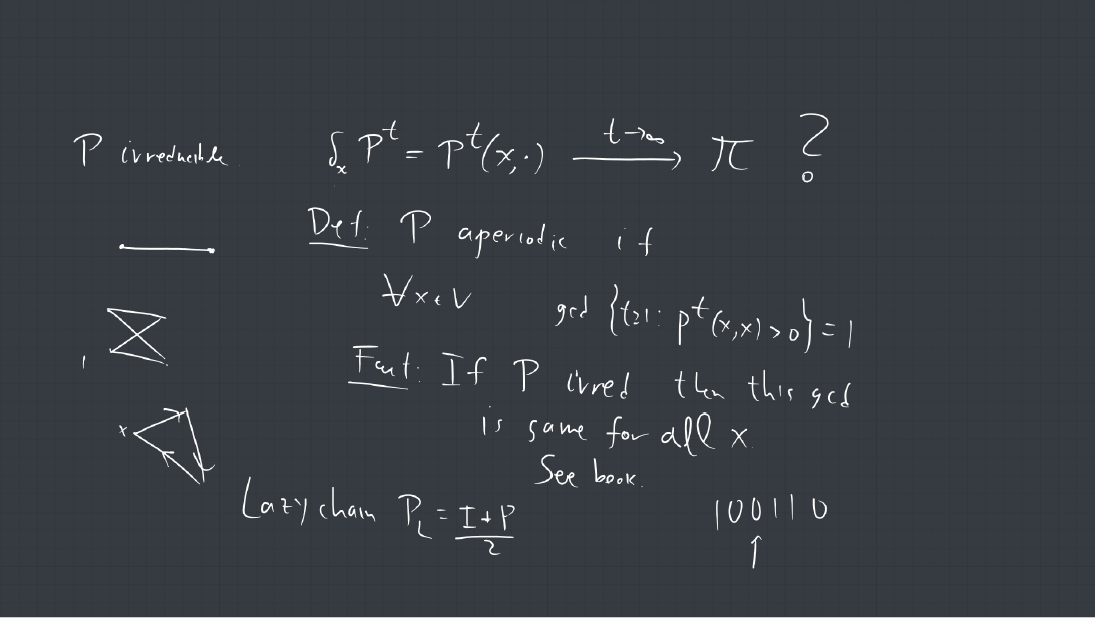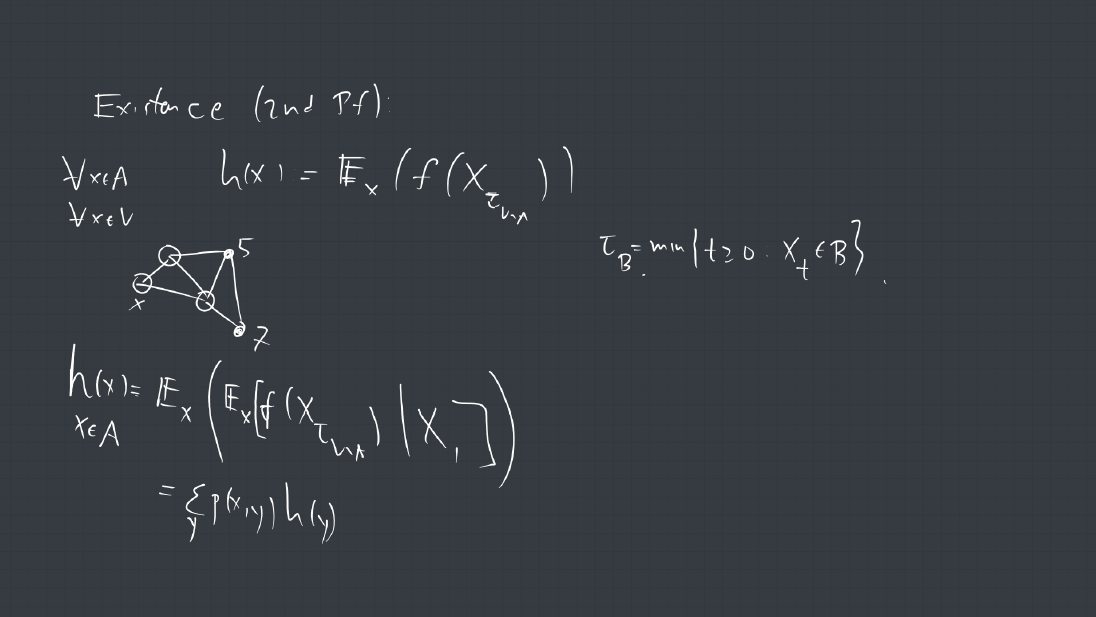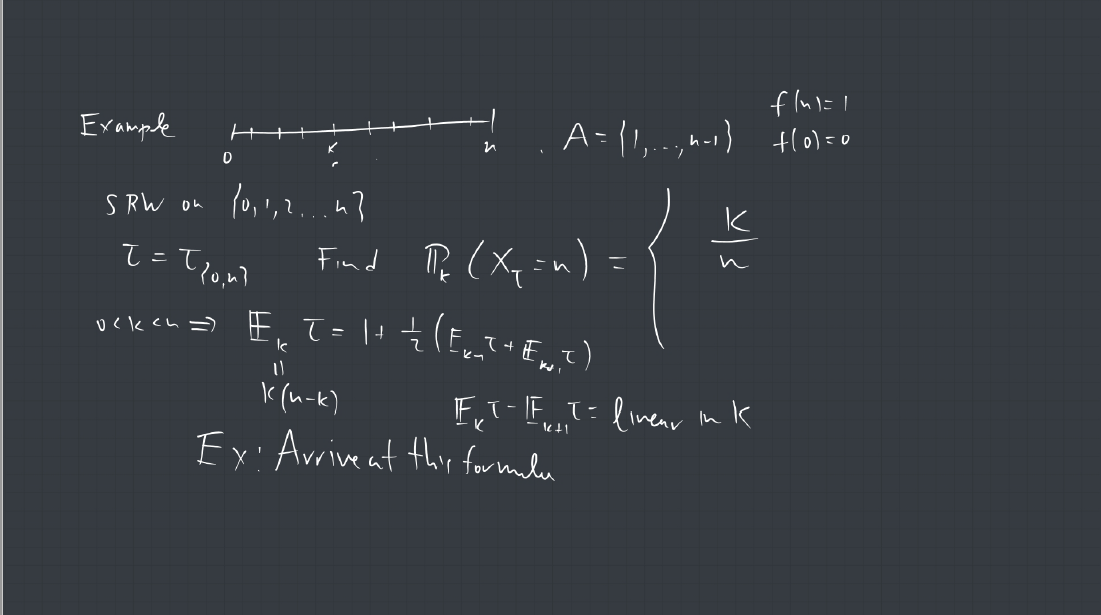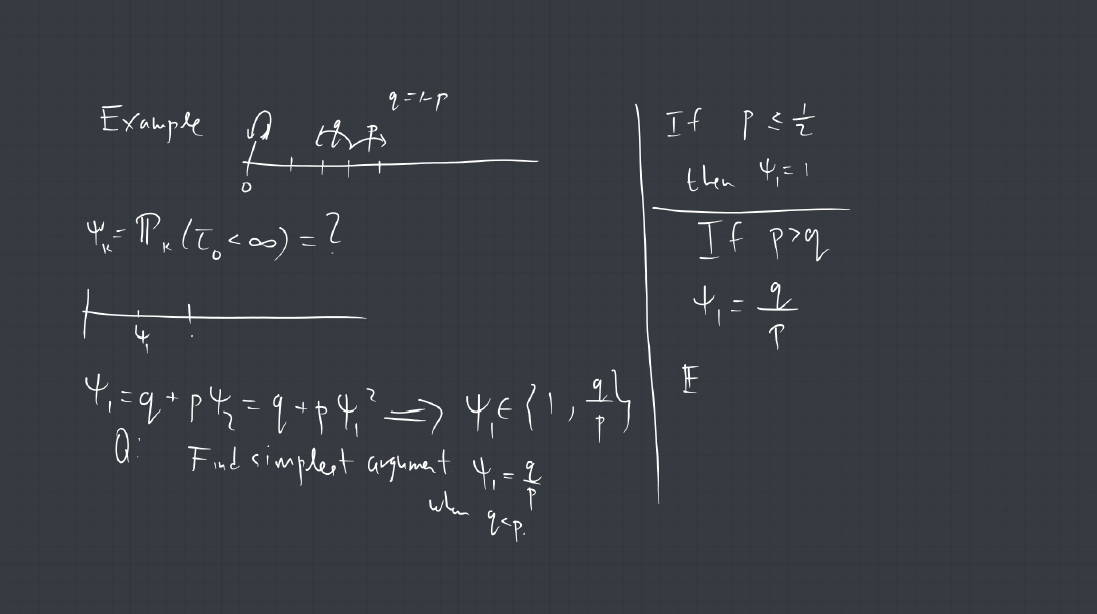1. A connected graph is a tree if it contains no cycles. Show that every finite tree with at least two vertices must have at least two leaves. (a leaf is a vertex of degree 1).
2. A vertex coloring of a graph is called proper if every pair of adjacent vertices are assigned different colors. Consider the following Markov chain on the set of proper 3 colorings of a finite tree ![]() : At each step, a vertex
: At each step, a vertex ![]() of
of ![]() is selected uniformly at random, and is assigned randomly, uniformly one of the colors that does not appear among the neighbors of
is selected uniformly at random, and is assigned randomly, uniformly one of the colors that does not appear among the neighbors of ![]() . Show that this chain is irreducible.
. Show that this chain is irreducible.
3. Let ![]() be a transition matrix on a finite set
be a transition matrix on a finite set ![]() . Suppose that
. Suppose that ![]() is a stationary distribution for
is a stationary distribution for ![]() and
and ![]() . Show that
. Show that ![]()